(1) 불 논리

불 게이트(Boolean gate)는 불 함수(Boolean function)를 물리적으로 구현한 것으로 먼저 불 대수(Boolean algebra)부터 간략하게 살펴본다. 

 

[ 불 대수(Boolean algebra) ]

 

불 대수는 참/거짓, 1/0과 같은 불(2진수) 값을 다루는 대수학이다.

불 함수는 2진수를 입력받아 2진수를 출력하는 함수다. 

 

불 함수를 정의하는 가장 쉬운 방법은 함수의 입력값들과 결괏값을 나란히 쓰는 방법인데 이 방법을 진리표 표현이라고 한다.

진리표 예시

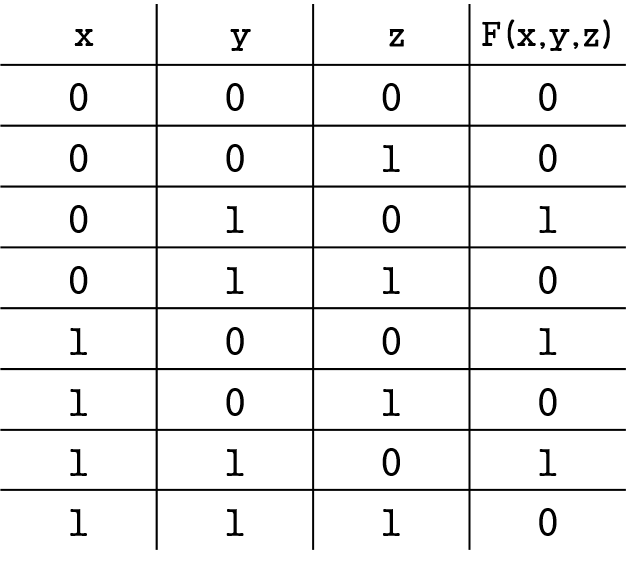
앞의 세 열은 함수 입력값이 될 수 있는 모든 2진 값 조합을 나타낸다.

마지막 열은 2^n개의 튜플 v1,v2,,,,,vn 에 대한 함수 값 f(v1,,,,vn)이다.

 

앞의 세 열 작성 요령은 2^n개의 절반씩 0,1을 작성해주면 된다. 

위 표의 예시를 들면 n=3이므로 

첫번째 열에서는 2^3 = 8의 절반인 4번 0을 쓰고 그 다음에는 또 1을 4번 써준다. (00001111)

두번째 열에서는 이제는 8의 절반의 절반인 2만큼 0과 1을 반복해서 써준다. 즉, 2번 0을 반복하고 다시 2번 1을 반복하고..(00110011)

이 과정을 세 번째 열처럼 한번씩 반복될 때까지 해주면 된다.  (01010101)

 

말로 설명해서 좀 어려워보여도 진리표를 몇 번 작성하다보면 적응이 금방 되는 부분이다.

 

[ 불 표현식 ]

AND : x • y

OR : x + y

XOR : x ⊕ y

XNOR : x ⊙ y

 

[ 정준 표현(canonical representation) ]

 

위 예시함수에서 함수의 값이 1인 부분을 살펴보자

1. (x,y,z) = (0,1,0)

2. (x,y,z) = (1,0,0)

3. (x,y,z) = (1,1,0)

 

이를 0인 경우 기호 위에다가 -를 붙여서 표현하고 1인 경우에는 기호 그대로 표현하면 된다.

1번의 경우 : x ̅yz ̅

2번의 경우 : xy ̅z ̅

3번의 경우 : xyz ̅

 

이는 곧 함수 표현식으로 작성된다.

f(x,y,z) = x ̅yz ̅ + xy ̅z ̅+xyz ̅

 

이로서 아무리 복잡한 불 함수라도 And, Or, Not 의 3가지 불 연산만으로 표현 가능하다는 중요한 결론을 얻게 된다.

 

NAND(NOT+AND)함수와 NOR(NOT+OR)함수는 흥미로운 성질이 있는데

바로 AND, OR, NOT함수를 모두 NAND 또는 NOR 함수만으로 만들 수 있다는 뜻이다.

 

EX) x OR y = (x NAND x) NAND (y NAND y)

 

그런데 모든 불 함수는 AND, OR NOT 연산으로만 이루어진 정준 표현식으로 작성할 수 있으므로 결국, 모든 불 함수는 NAND 함수만으로 또는 NOR 함수만으로 표현할 수 있다는 것이다.