What is Diffusion?
Diffusion(확산)이란 위키피디아의 정의에 따르면 다음과 같이 정의된다.
확산(Diffusion)은 액체나 기체에 다른 물질이 섞이고 그것이 조금씩 번져가다가 마지막에는 일률적인 농도로 바뀌는 현상이다.
물 속에 잉크를 떨어뜨렸을 때 시간이 지나면 지날수록 점점 퍼지는 현상을 생각해볼 수 있을 것이다. 위 정의를 다시 따와서 해석해보면 액체에 잉크가 섞이고 그것이 조금씩 번져다가 마지막에는 일률적인 농도로 바뀌는 현상이다.
Diffusion on 1-D
이제 정의를 알아봤으니 예시를 통해 좀 더 자세히 생각해보자.
1차원 공간에서의 diffusion을 생각해보자.

위와 같이 L의 길이를 가지는 막대가 존재한다. 여기서 막대의 어떠한 위치에 불을 지펴서 열을 가해준다고 가정하자. 이때 시간이 지남에 따라 막대의 온도 변화는 어떻게 나타날까?
$u(x,t)$가 $t$시점에서 막대의 $x$ 지점에서의 온도(혹은 확산하는 물질의 concentration. 지금의 경우에는 열이 확산하는 것이라고 생각해볼 수 있다.) 그러면 다음과 같은 Diffusion Equation으로 막대의 온도 변화를 정의할 수 있다.
$$ \frac{\partial u}{\partial t}=D\frac{\partial^2 u}{\partial x^2} $$
이때 D는 diffusion rate라고 하는 coefficient이다. 이와 같은 Equation은 initial value와 boundary condition 역시 제공해줘야 한다.
식을 해석해보자면 시간에 따른 온도변화량은 point에 대한 2차미분 즉, 어떠한 point에서 자기 주변값의 평균값과의 차이에 비례한다는 이야기가 된다. 예를 들어 생각해보면 t시점에서 어떤 point의 다음 t+1 시점에서의 온도변화는 주변값의 온도에 따라 정의된다는 것이다. 주변 지점의 온도가 높으면 t+1시점에서 어떤 point의 온도는 상승할 것이고, 반대면 하강할 것이다.
위 식을 더 높은 차원으로 일반화해서 생각해보면 아래와 같이 Laplacian operator($\nabla$)를 이용해서 정의해줄 수 있다.
$$ \frac{\partial u}{\partial t}=D\nabla^2 u $$
만약 3차원의 경우 Laplacian operator는 다음과 같이 정의된다.

Diffusion on Graph
이제 이러한 diffusion을 Graph domain에서 생각해보자.
어떠한 diffusing substance(e.g. 열)가 graph 의 edge를 따라서 움직인다고 생각해보자. 즉, node에서 node로 가는 것이라고 생각해보자. 이렇게 되면 domain은 continuous하지 않고 discrete한 domain이 된다.

c가 edge에서의 diffusion rate라고 생각해보자.
- $c(u_j-u_i)dt$ : time period dt동안 j → i 로 가는 substance의 양
- $c(u_i-u_j)dt$ : time period dt동안 i → j 로 가는 substance의 양
다시 말해 아래와 같이 수식으로 정리할 수 있다.

이때 node i에서 시작하는 그리고 i로 가는 diffusion을 고려하기 위해서는 다른 노드들도 고려해야되는데, 이때 그래프의 connectivity가 adjacency matrix에 연결되어있으므로 이를 이용하여 node i와 연결된 node들을 고려해주는 diffusion 식을 작성하면 아래와 같다.

이를 다시 작성하게 되면,
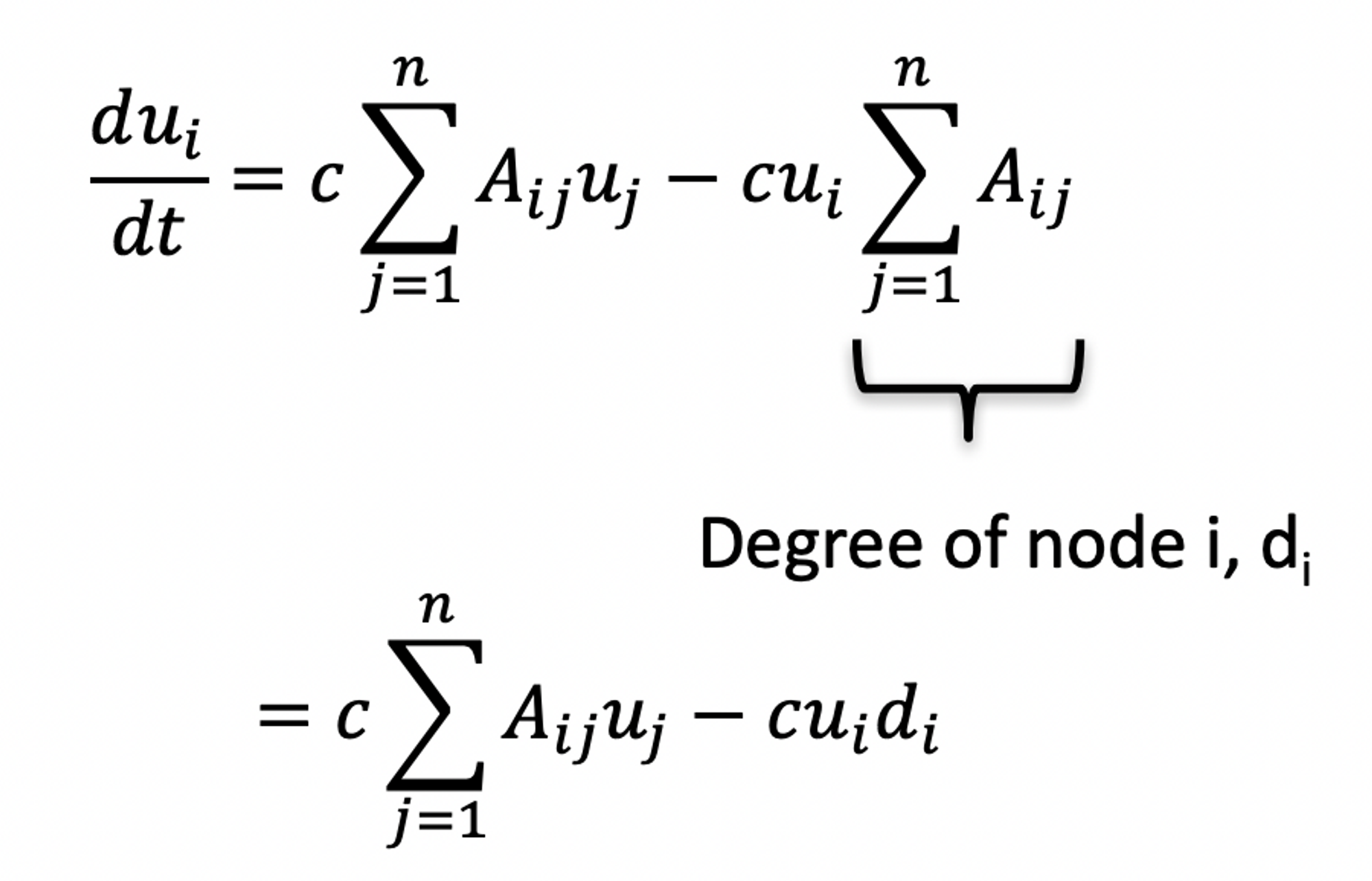
이제 Kronecker delta인 $ \delta_{ij} $를 써서 식을 다시 정리해보면,

아래와 같이 작성해줄 수 있다.

즉, $cu_id_i$ 와 같이 $i$ 노드에 대한 표현식을 이웃노드인 $j$ 노드에 대한 표현식으로 바꿔 써줄 수 있다.
그리고 여기서 조금 더 정리를 해주면 $u$를 $n$차원의 벡터로 놓고, Degree matrix를 $n\times n$ matrix로 생각해보면,

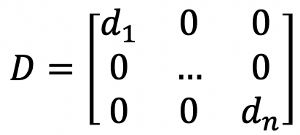
아래와 같이 좌항과 우항을 정리해줄 수 있다.
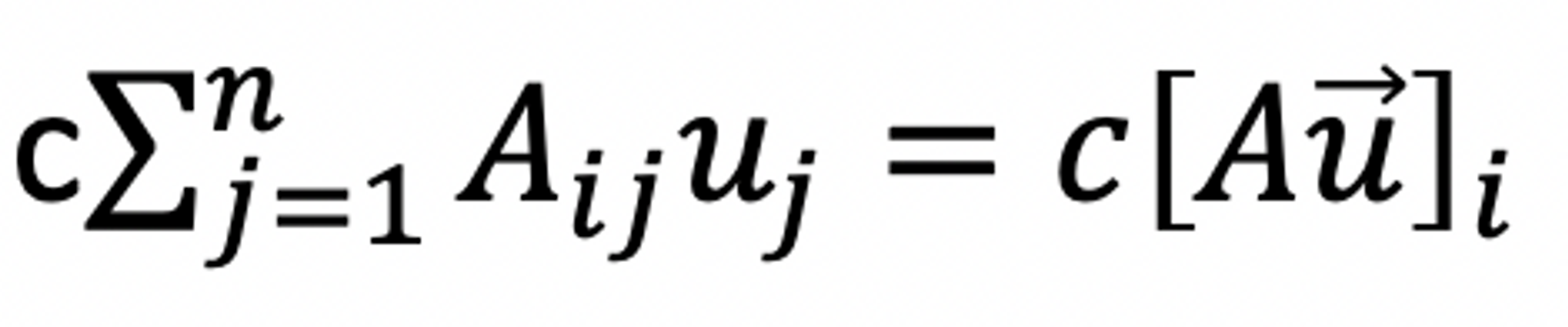

따라서 최종 식을 다시 아래와 같이 matrix multiplication 꼴로 정의해줄 수 있게 된다.

최종 식을 보면 어딘가 익숙한 식이 보이지 않는가? 바로 Graph Laplacian Matrix ( $L=D-A$ )가 보이게 된다.
항상 Graph Laplacian Matrix는 왜 $D-A$로 정의될 수 있는가가 궁금했었는데 그 이유 또한 이번 글을 정리하면서 알 수 있게 되었다.